The Trapping Rainwater problem is a classic coding challenge that tests your understanding of arrays, dynamic programming, and two-pointer techniques. The problem involves calculating the amount of water that can be trapped between different heights of bars, which are represented by an array of non-negative integers. These bars can trap rainwater in the valleys created between higher bars, much like a container.
In this article, we will break down the problem, provide an intuitive approach to solve it, and explore an efficient solution using the two-pointer technique. By the end of this guide, you will have a clear understanding of how to tackle the Trapping Rainwater problem using code.
Table of Contents
Brute Force Solution for Trapping Rainwater: Naive Approach
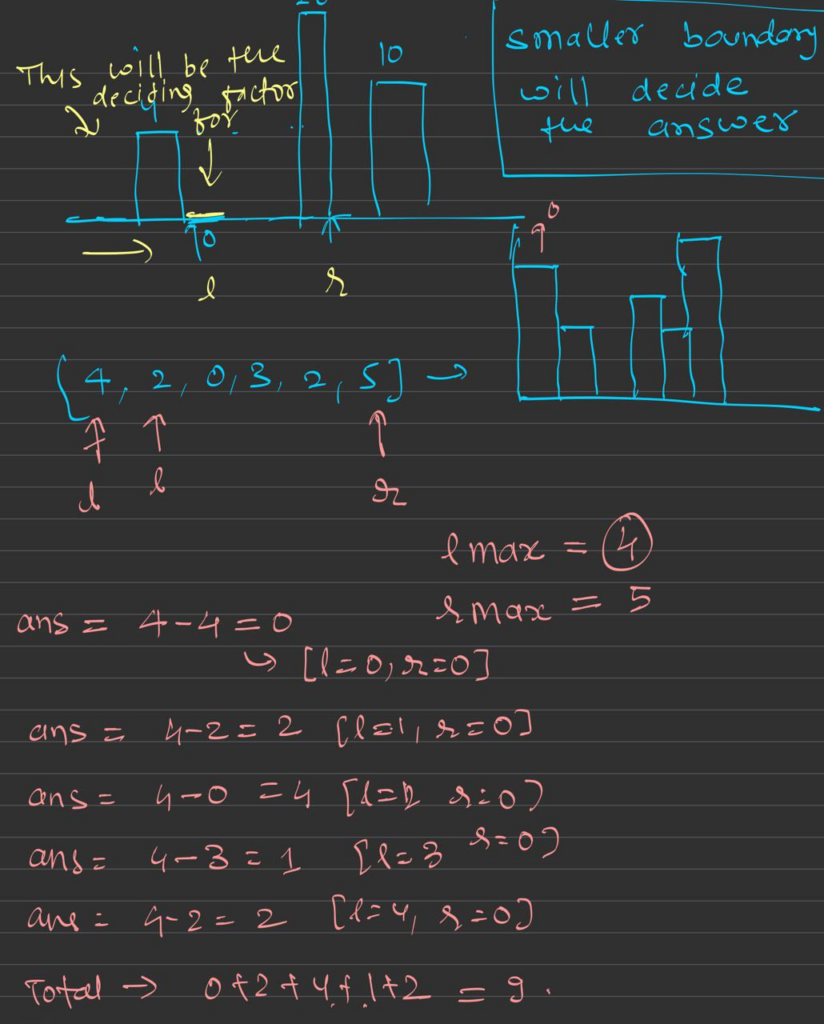
In the Trapping Rainwater problem, a simple and brute-force approach involves calculating the left and right maximum heights for each element in the array. This naive method is easy to understand but inefficient in terms of time complexity. Let’s explore this approach in detail.
Approach:
The core idea behind this brute force method is to look at every element in the array and figure out the tallest bars on its left and right sides. By doing this, we can compute how much water would be trapped above that element. The trapped water at any given position is determined by the difference between the shorter of the two heights (left max and right max) and the current bar’s height. If the height of the bar is smaller than the shorter of the two maximum heights, it implies water can be trapped above it.
Steps:
- For each bar, identify the tallest bar to its left.
- Similarly, identify the tallest bar to its right.
- The water trapped above the current bar will be the difference between the shorter of these two heights and the height of the bar itself.
- Sum up the trapped water across all the bars to get the total water trapped.
Time Complexity:
- For each bar, we calculate the maximum height to the left and right, which requires a scan of the entire array for each element. This results in a time complexity of O(n^2).
Space Complexity:
- This solution doesn’t require any extra space apart from a few variables, so the space complexity is O(1).
Code Implementation (Naive Brute Force)
def trap(height):
n = len(height)
total_water = 0
# Traverse each element of the array
for i in range(1, n - 1):
# Find the maximum height to the left of the current element
left_max = max(height[:i])
# Find the maximum height to the right of the current element
right_max = max(height[i + 1:])
# Calculate the trapped water at the current index
water_at_i = min(left_max, right_max) - height[i]
# If water can be trapped, add it to the total water trapped
if water_at_i > 0:
total_water += water_at_i
return total_water
# Example usage
height = [0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1]
print(f"Water trapped: {trap(height)}")
Explanation:
- Finding Left Maximum: For each bar, we calculate the maximum height of the bars to its left using the
max()function:left_max = max(height[:i]). - Finding Right Maximum: Similarly, we compute the maximum height of the bars to the right of the current bar:
right_max = max(height[i+1:]). - Water Calculation: For each index
i, we determine the amount of water trapped at that position as the difference between the smaller of the two maximum heights (left_maxandright_max) and the current height. If the result is positive, water is trapped, and we add this value to the total amount of water.
Limitations of the Naive Approach:
While this brute-force method is easy to understand, it is not efficient for large input sizes. The time complexity of O(n^2) makes it impractical for arrays with a large number of elements. In such cases, more optimized approaches such as the two-pointer technique or dynamic programming are preferred to solve the problem efficiently.
Optimized Approach: Using Prefix and Suffix Maximum Arrays for Trapping Rainwater
A more efficient solution to the Trapping Rainwater problem can be achieved by using two auxiliary arrays: prefix max and suffix max. This approach reduces the time complexity to O(n) and uses O(n) space, making it a significant improvement over the brute force method.
Approach:
The basic idea of this optimized approach is to compute the maximum height to the left and right of each bar using two separate arrays:
- Prefix Max Array: This array stores the maximum height encountered from the left up to each index.
- Suffix Max Array: This array stores the maximum height encountered from the right up to each index.
Once these two arrays are computed, the trapped water at any index can be calculated by taking the minimum of the corresponding values in the prefix max and suffix max arrays, and subtracting the height of the bar at that index.
Steps:
- Prefix Max Calculation: Iterate through the array from left to right and compute the maximum height at each index from the left side.
- Suffix Max Calculation: Iterate through the array from right to left and compute the maximum height at each index from the right side.
- Trapping Water Calculation: For each bar, the amount of water trapped above it is determined by the formula: Water at index=min(prefix_max[i],suffix_max[i])−height[i]\text{Water at index} = \min(\text{prefix\_max}[i], \text{suffix\_max}[i]) – \text{height}[i] If the result is positive, water is trapped; otherwise, no water is trapped at that index.
- Sum up the trapped water for all indices.
Time Complexity:
- O(n): The algorithm makes three passes through the array (one for the prefix max, one for the suffix max, and one for calculating the trapped water), resulting in a linear time complexity.
Space Complexity:
- O(n): We use two additional arrays (
prefix_maxandsuffix_max) to store the maximum heights, which requires O(n) space.
Code Implementation (Prefix and Suffix Max)
def trap(height):
n = len(height)
if n == 0:
return 0
# Initialize arrays for prefix max and suffix max
prefix_max = [0] * n
suffix_max = [0] * n
# Fill the prefix_max array
prefix_max[0] = height[0]
for i in range(1, n):
prefix_max[i] = max(prefix_max[i - 1], height[i])
# Fill the suffix_max array
suffix_max[n - 1] = height[n - 1]
for i in range(n - 2, -1, -1):
suffix_max[i] = max(suffix_max[i + 1], height[i])
# Calculate the total amount of trapped water
total_water = 0
for i in range(n):
# Calculate trapped water at each index
water_at_i = min(prefix_max[i], suffix_max[i]) - height[i]
if water_at_i > 0:
total_water += water_at_i
return total_water
# Example usage
height = [0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1]
print(f"Water trapped: {trap(height)}")
Explanation:
- Prefix Max Array:
- We iterate from left to right, and at each index, we store the maximum height encountered up to that point. This helps in determining the maximum bar height to the left of any given bar.
- Suffix Max Array:
- We iterate from right to left, and at each index, we store the maximum height encountered from that point to the end. This helps in determining the maximum bar height to the right of any given bar.
- Water Calculation:
- For each element, we compute the amount of trapped water by calculating the minimum of the prefix and suffix max values at that index, and subtracting the height of the current bar. If this value is positive, water can be trapped; if it’s zero or negative, no water can be trapped at that index.
Example Walkthrough:
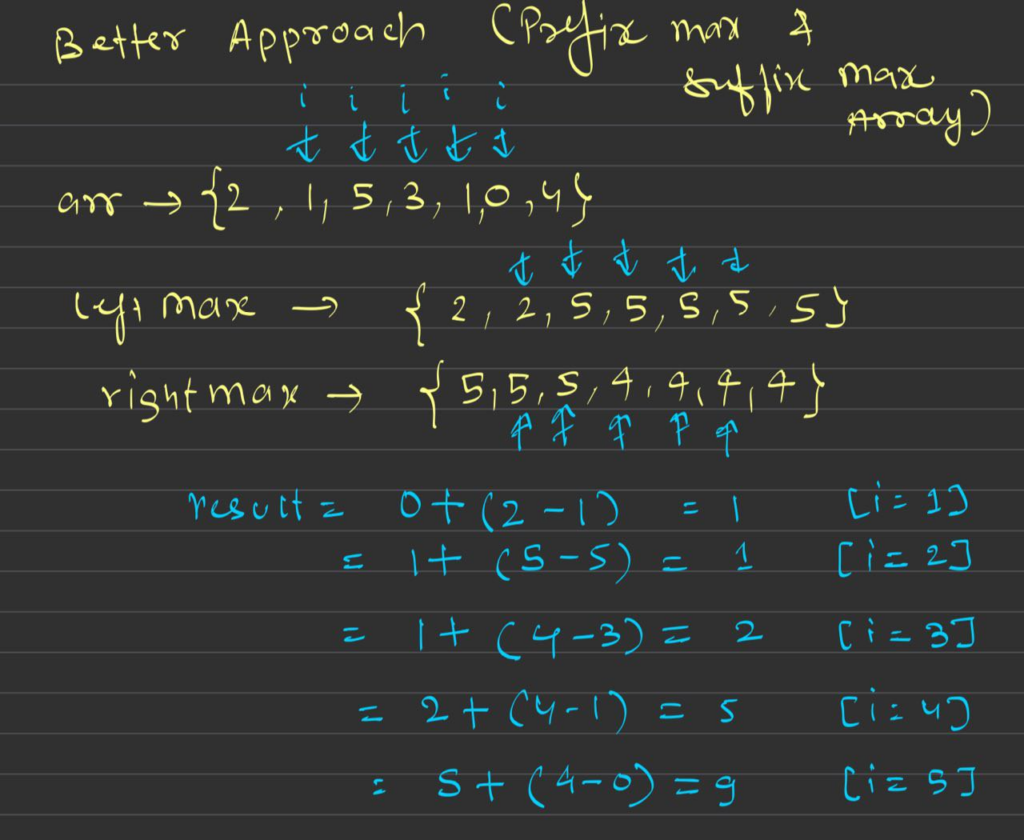
Two Pointer Approach for Trapping Rainwater: Optimized and Efficient Solution
The Trapping Rainwater problem can be solved even more efficiently using the Two Pointer Approach. This approach significantly improves performance, reducing the time complexity to O(n) and using O(1) space. It’s one of the most optimal solutions for this problem, and understanding how to implement it is crucial for solving large-scale problems efficiently.
Approach:
In the Two Pointer Approach, we utilize two pointers to traverse the array: one starting from the leftmost index (left) and the other from the rightmost index (right). The idea is to compute the amount of trapped water by comparing the heights at these two pointers and gradually moving towards the center of the array.
Steps:
- Initialize Pointers: Start by setting
leftto 0 (beginning of the array) andrightton-1(end of the array). - Track Maximum Heights: Maintain two variables,
left_maxandright_max, which store the maximum heights encountered so far from the left and right, respectively. - Calculate Water Trapped:
- Compare the heights at the
leftandrightpointers. - If the height at
leftis smaller than or equal to the height atright, then:- If the height at
leftis greater than or equal toleft_max, updateleft_max. - Otherwise, calculate the trapped water at the
leftpointer usingleft_max - height[left]. - Move the
leftpointer one step to the right.
- If the height at
- If the height at
rightis smaller than the height atleft, do the same for therightpointer by updatingright_maxand calculating the trapped water.
- Compare the heights at the
- Continue Until Pointers Meet: Continue this process until the
leftandrightpointers meet. The total water trapped will be the sum of water trapped at each step.
Time Complexity:
- O(n): The algorithm only requires a single pass through the array, resulting in linear time complexity.
Space Complexity:
- O(1): This approach uses only a few variables (
left,right,left_max,right_max, andtotal_water), so it operates with constant space complexity.
Code Implementation (Two Pointer Approach)
def trap(height):
n = len(height)
if n == 0:
return 0
left, right = 0, n - 1
left_max, right_max = height[left], height[right]
total_water = 0
while left <= right:
# Compare the heights at the two pointers
if height[left] <= height[right]:
# If the height at left is less, process the left pointer
if height[left] >= left_max:
left_max = height[left]
else:
total_water += left_max - height[left]
left += 1
else:
# If the height at right is less, process the right pointer
if height[right] >= right_max:
right_max = height[right]
else:
total_water += right_max - height[right]
right -= 1
return total_water
# Example usage
height = [0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1]
print(f"Water trapped: {trap(height)}")
Explanation:
- Pointer Initialization:
- We start with the
leftpointer at the beginning of the array (left = 0) and therightpointer at the end (right = n-1).
- We start with the
- Max Heights Tracking:
- We keep track of the highest bars encountered from the left and right sides using
left_maxandright_max. These values are updated whenever we encounter a new taller bar at the respective pointers.
- We keep track of the highest bars encountered from the left and right sides using
- Water Calculation:
- If the height at
leftis smaller than or equal to the height atright, we focus on theleftpointer:- If the current height is greater than or equal to
left_max, we updateleft_max. - If the current height is smaller than
left_max, we calculate the trapped water at this position and move theleftpointer rightward.
- If the current height is greater than or equal to
- If the height at
rightis smaller thanleft, we perform similar steps for therightpointer, updatingright_maxand calculating trapped water.
- If the height at
- Termination:
- The loop continues until the
leftpointer surpasses therightpointer, ensuring all elements are processed.
- The loop continues until the
Example Walkthrough: