The Subarray Sum Equal to K problem is a popular coding challenge that requires you to find the total number of continuous subarrays whose sum is equal to a given target value K. This problem is widely asked in coding interviews and is essential for anyone looking to master array manipulation and subarray problems.

In this article, we will discuss two approaches for solving the Subarray Sum Equal to K problem:

1. Brute Force Approach: A straightforward but inefficient way to solve the problem.
2. Optimal Approach Using Prefix Sum: A more efficient approach that reduces the time complexity, making it suitable for larger inputs.

We will explain both methods using C++ and focus on the efficiency improvements achieved with the Prefix Sum technique.

Problem Definition:

Given an integer array nums and an integer k, you need to find the number of continuous subarrays whose sum equals k. A subarray is a contiguous part of the array.

Brute Force Solution

In the brute force approach, we generate all possible subarrays and compute their sums. If the sum matches k, we increase the count.

Steps:

1. For each element in the array, consider it as the starting point of a potential subarray.
2. From that starting point, iterate over all subsequent elements to form subarrays.
3. Calculate the sum of each subarray and check if it is equal to k.

Time Complexity:

• O(n^2): We generate all possible subarrays, and for each subarray, we compute the sum, leading to a quadratic time complexity.

Space Complexity:

• O(1): The brute force solution uses only a few variables for counting and summing.

Brute Force Code Implementation (C++)

#include <iostream>
#include <vector>

using namespace std;

int subarraySumBruteForce(vector<int>& nums, int k) {
    int count = 0;
    int n = nums.size();

    // Iterate over all possible starting points of subarrays
    for (int i = 0; i < n; i++) {
        int sum = 0;
        
        // For each starting point, sum all possible subarrays
        for (int j = i; j < n; j++) {
            sum += nums[j];
            
            // If the sum equals k, increment the count
            if (sum == k) {
                count++;
            }
        }
    }
    
    return count;
}

int main() {
    vector<int> nums = {1, 2, 3, 4, 1};
    int k = 5;
    
    cout << "Subarrays with sum equal to " << k << ": " << subarraySumBruteForce(nums, k) << endl;
    return 0;
}

Explanation:

1. Outer Loop: The outer loop iterates over each element of the array and treats it as the start of a potential subarray.
2. Inner Loop: The inner loop generates subarrays by extending from the current starting point and calculates their sums.
3. Count Matching Subarrays: If the sum of a subarray equals k, we increment the count.

While this approach is simple, it is not efficient, especially for larger arrays due to its O(n^2) time complexity.

Approach 2: Optimal Approach Using Prefix Sum

The optimal solution leverages the Prefix Sum technique, which helps reduce the time complexity from O(n^2) to O(n). Instead of calculating the sum of every subarray directly, we can use a running sum to track the sum of elements from the beginning of the array up to the current index.

Key Insights:

1. Prefix Sum Array: The prefix sum at index i is the sum of elements from nums[0] to nums[i].
2. Difference of Prefix Sums: To find the sum of any subarray nums[i..j], we can compute it as: sum(i,j)=prefix[j]−prefix[i−1]\text{sum}(i, j) = \text{prefix}[j] – \text{prefix}[i-1]
3. Target Subarray Sum: If prefix[j] - prefix[i-1] == k, then we know the sum of the subarray nums[i..j] is k.

Steps:

1. Initialize a prefix_sum variable to 0 and a hash map (or unordered_map) to store the frequency of prefix sums.
2. As you iterate over the array, update the prefix_sum with the current element.
3. For each prefix_sum, check if there exists a previous prefix sum that satisfies prefix_sum - k (this indicates that a subarray with sum k exists).
4. If such a prefix sum is found, increase the count by the frequency of that previous prefix sum.

Time Complexity:

• O(n): We traverse the array once and use the hash map for constant time lookups.

Space Complexity:

• O(n): We use a hash map to store the frequency of prefix sums.

Prefix Sum Code Implementation (C++)

#include <iostream>
#include <unordered_map>
#include <vector>

using namespace std;

int subarraySumPrefixSum(vector<int>& nums, int k) {
    unordered_map<int, int> prefix_sum_count;
    int count = 0;
    int prefix_sum = 0;

    // Initialize with 0 to handle the case when a subarray starts from the first element
    prefix_sum_count[0] = 1;

    for (int num : nums) {
        // Update the prefix sum
        prefix_sum += num;

        // Check if there exists a prefix sum that satisfies prefix_sum - k
        if (prefix_sum_count.find(prefix_sum - k) != prefix_sum_count.end()) {
            count += prefix_sum_count[prefix_sum - k];
        }

        // Store the frequency of the current prefix sum
        prefix_sum_count[prefix_sum]++;
    }

    return count;
}

int main() {
    vector<int> nums = {1, 2, 3, 4, 1};
    int k = 5;

    cout << "Subarrays with sum equal to " << k << ": " << subarraySumPrefixSum(nums, k) << endl;
    return 0;
}

Explanation:

1. Prefix Sum Calculation: As we iterate through the array, we maintain the running sum (prefix_sum) of all elements seen so far.
2. Hash Map Lookup: We use an unordered map (prefix_sum_count) to store how many times each prefix_sum has occurred. For every element, we check if the difference prefix_sum - k has been seen before. If it has, it means that there are subarrays ending at the current element whose sum equals k.
3. Count Subarrays: Each time we find a matching prefix sum, we add the frequency of that sum to the count of subarrays.

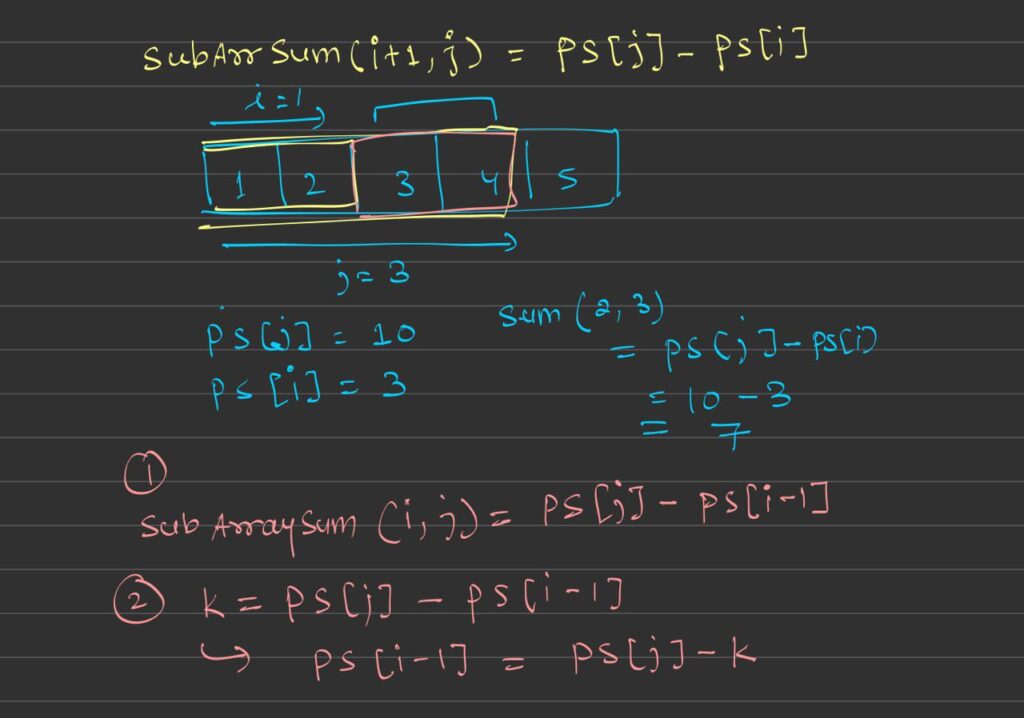
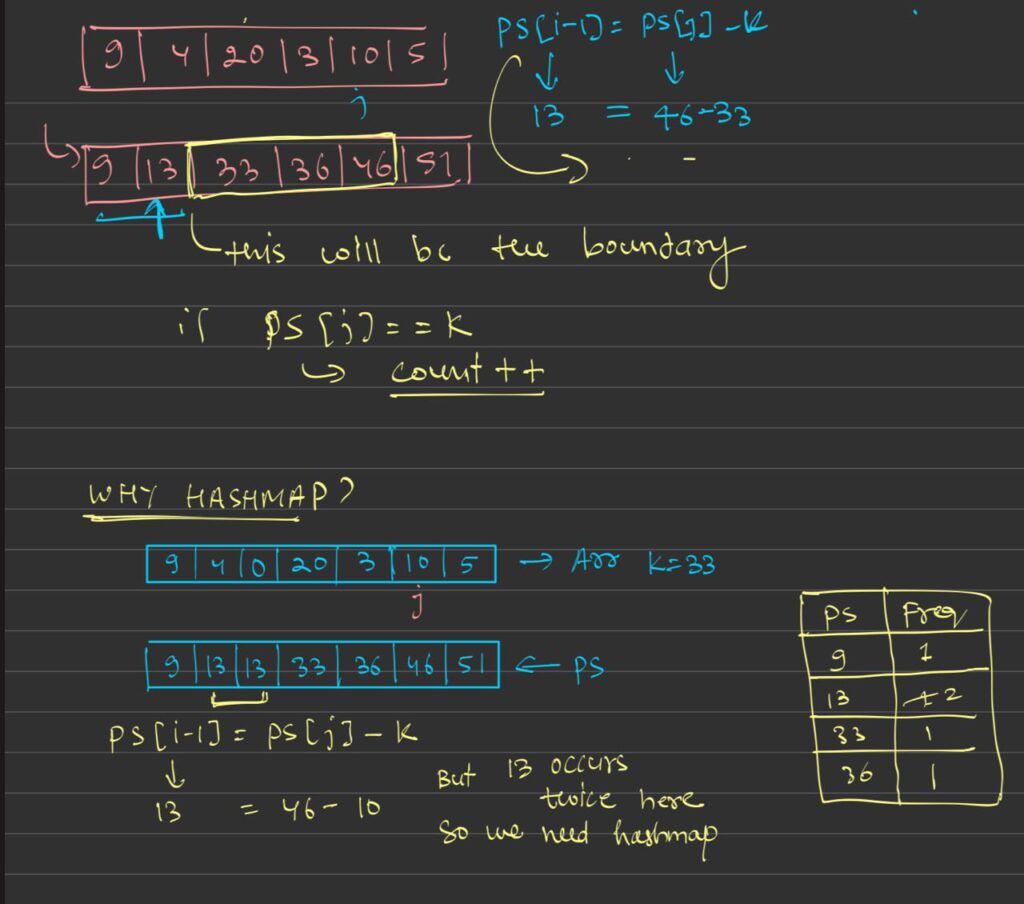
Conclusion:

The Subarray Sum Equal to K problem can be solved efficiently using two approaches in C++:

• The Brute Force approach is easy to understand but inefficient, with a time complexity of O(n^2).
• The Optimal Approach Using Prefix Sum significantly improves the time complexity to O(n), using a hash map to store prefix sums and efficiently count matching subarrays.

The Prefix Sum technique is an essential tool for optimizing array-based problems, especially when it comes to calculating the sum of subarrays. By leveraging this technique, we can solve the Subarray Sum Equal to K problem in an optimal manner, making it highly scalable for large inputs.