Introduction

The K-th missing number problem is a common challenge in coding competitions and technical interviews. In this problem, you are given a sorted array of distinct integers and an integer k, and the goal is to determine the K-th missing number from the sequence.

Problem Statement

You are given a sorted array arr of distinct integers and an integer k. The task is to find the K-th positive integer that is missing from the array.

Example:

k = 5
Array = [12, 3, 4, 7, 11]

Understanding the Approach

A straightforward approach is to calculate the ideal sequence without any missing numbers. Then, compare it with the given array to find the missing numbers.

Ideal Sequence:

[1, 2, 3, 4, 5, 6, 7, 8, ...]

Optimized Algorithm to Find the K-th Missing Number

Step 1: Use Binary Search

• Perform a binary search on the array to determine how many numbers are missing at any given index.
• Calculate how many numbers are missing using the formula: Missing numbers till index i: arr[i] - (i + 1)
• Adjust the search range based on whether the missing count at mid is greater than or less than k.

Step 2: Determine the Exact Missing Number

• If k missing numbers are not found by the end of the array, calculate using the last index. Formula: arr[high] + (k - missing_count)

Example Walkthrough

k = 5
arr = [12, 3, 4, 7, 11]

• Perform binary search to find the point where the missing count reaches k.
• Adjust pointers (low and high) until the desired missing number is located.

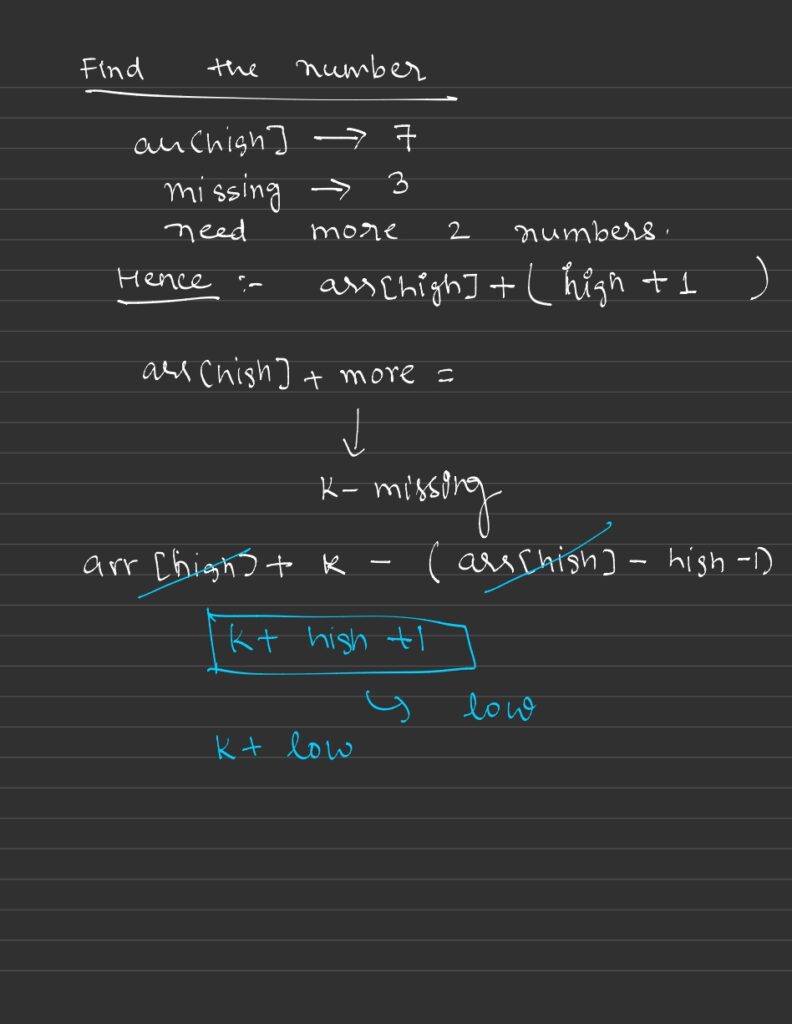
Efficient Code Implementation

Here is an optimized implementation using binary search:

def find_kth_missing(arr, k):
    low, high = 0, len(arr) - 1
    while low <= high:
        mid = (low + high) // 2
        missing_count = arr[mid] - (mid + 1)
        if missing_count < k:
            low = mid + 1
        else:
            high = mid - 1

    return high + 1 + k

# Example Usage
arr = [12, 3, 4, 7, 11]
k = 5
print("K-th Missing Number:", find_kth_missing(arr, k))

Conclusion

The binary search approach is an efficient way to find the K-th missing number with a time complexity of O(log n). By understanding the missing number concept using midpoints and adjusting search bounds, you can solve this problem quickly and accurately.

Try implementing this algorithm with different inputs to deepen your understanding and improve your problem-solving skills!