To solve the problem of finding the first negative number in every window of size k in an array, we can use a sliding window approach. I’ll explain the brute force, better, and optimal approaches in C++, providing code along with a dry run for each.

Problem Statement:

Given an array arr[] and an integer k, find the first negative number in every window of size k. If there is no negative number in the window, print 0.

1. Brute Force Approach

In the brute force approach, we will loop through each window of size k and find the first negative number. This approach has a time complexity of O(n * k) because for each window of size k, we are scanning through the elements.

Code:

#include <iostream>
#include <vector>
#include <climits>

using namespace std;

void firstNegativeNumberBruteForce(vector<int>& arr, int k) {
    int n = arr.size();
    for (int i = 0; i <= n - k; i++) {
        bool found = false;
        for (int j = i; j < i + k; j++) {
            if (arr[j] < 0) {
                cout << arr[j] << " ";
                found = true;
                break; // exit as soon as we find the first negative number
            }
        }
        if (!found) {
            cout << "0 "; // No negative number in the window
        }
    }
    cout << endl;
}

int main() {
    vector<int> arr = {12, -1, -7, 8, -15, 30, 16, 28};
    int k = 3;
    firstNegativeNumberBruteForce(arr, k);
    return 0;
}

Explanation:

• We iterate through each window of size k.
• For each window, we look for the first negative number.
• If no negative number is found, we print 0.

Dry Run:

For arr = [12, -1, -7, 8, -15, 30, 16, 28] and k = 3:

1. Window 1: [12, -1, -7] → The first negative number is -1. Print -1.
2. Window 2: [-1, -7, 8] → The first negative number is -1. Print -1.
3. Window 3: [-7, 8, -15] → The first negative number is -7. Print -7.
4. Window 4: [8, -15, 30] → The first negative number is -15. Print -15.
5. Window 5: [-15, 30, 16] → The first negative number is -15. Print -15.
6. Window 6: [30, 16, 28] → No negative number, so print 0.

Output:

-1 -1 -7 -15 -15 0

Time Complexity:

• O(n * k) where n is the length of the array, and k is the window size.

2. Better Approach (Using a Queue)

In the better approach, we can optimize the brute force solution by using a queue to store the indices of negative numbers. This reduces the time complexity to O(n), as we are iterating through the array only once.

Explanation of Better Approach:

• We maintain a deque (dq) to store indices of negative numbers.
• For each new window, we:
  • Remove elements from the front of the deque that are out of the current window.
  • Add the current negative number to the deque.
  • Output the first negative number in the deque or 0 if there are no negative numbers.

class Solution {
  public:
    vector<int> FirstNegativeInteger(vector<int>& arr, int k) {
        // write code here
        deque<int>dq;
        vector<int>ans;
        int n = arr.size();
        
        // Process the first window
        for(int i = 0; i < k; i++) {
            if(arr[i] < 0) dq.push_back(i);
        }
        
        // Add the result for the first window
        if(!dq.empty()) ans.push_back(arr[dq.front()]);
        else ans.push_back(0);

        // Process the remaining windows
        for(int i = k; i < n; i++) {
            // Remove elements that are out of the current window
            while(!dq.empty() && dq.front() <= i - k) dq.pop_front();
            
            // Add the current element to the deque if it's negative
            if(arr[i] < 0) dq.push_back(i);
            
            // Add the result for the current window
            if(!dq.empty()) ans.push_back(arr[dq.front()]);
            else ans.push_back(0);
        }
        
        return ans;
    }
};

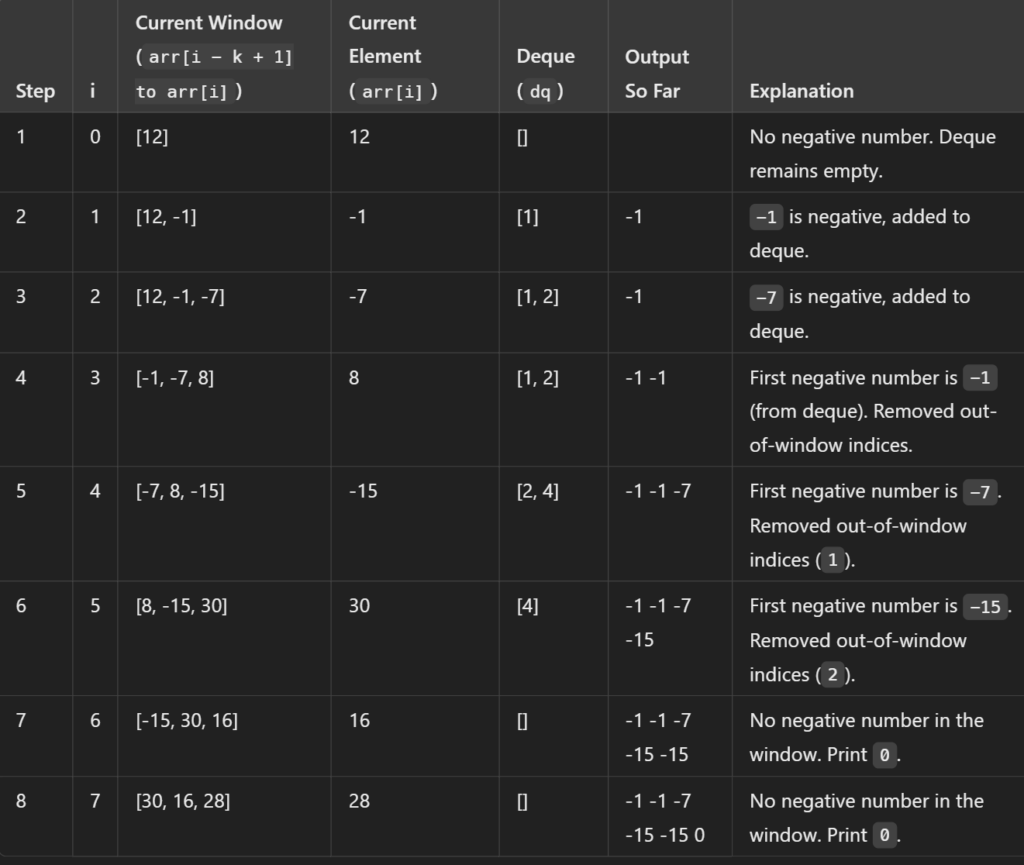
Dry Run Step-by-Step:

1. Initialize the deque to store indices of negative numbers in the window.
2. Process the first window (first k elements) separately:
   • The first window contains the elements [12, -1, -7] (i.e., indices 0 to 2).
   • We iterate through the window and find the negative numbers.
3. Start processing the rest of the array from index k to n-1.
   • For each new window, we:
     • Print the first negative number from the deque.
     • Remove indices that are out of the window.
     • Add the current negative number (if any) to the deque.

Dry Run for

arr = [12, -1, -7, 8, -15, 30, 16, 28] and k = 3:

1. First Window: Indices 0 to 2 ([12, -1, -7])
   • For indices 0 to 2, we check the negative numbers:
     • arr[0] = 12 → not negative.
     • arr[1] = -1 → negative, so add index 1 to the deque.
     • arr[2] = -7 → negative, so add index 2 to the deque.
   • Now, the deque contains indices [1, 2], pointing to -1 and -7.
   • First negative number: -1 (because index 1 is the first in the deque).
   • Output so far: -1
2. Window 2: Indices 1 to 3 ([-1, -7, 8])
   • Remove indices that are out of the window:
     • 1 is still in the window, so we don’t remove it.
     • 2 is still in the window, so we don’t remove it.
   • Add the new element arr[3] = 8, which is not negative.
   • The deque still contains indices [1, 2].
   • First negative number: -1 (because index 1 is still the first in the deque).
   • Output so far: -1 -1
3. Window 3: Indices 2 to 4 ([-7, 8, -15])
   • Remove indices that are out of the window:
     • Index 1 is out of the window, so we remove it.
   • The deque now contains [2] (pointing to -7).
   • Add the new element arr[4] = -15, which is negative, so we add index 4 to the deque.
   • The deque now contains [2, 4].
   • First negative number: -7 (because index 2 is still the first in the deque).
   • Output so far: -1 -1 -7
4. Window 4: Indices 3 to 5 ([8, -15, 30])
   • Remove indices that are out of the window:
     • Index 2 is out of the window, so we remove it.
   • The deque now contains [4] (pointing to -15).
   • Add the new element arr[5] = 30, which is not negative.
   • The deque still contains [4].
   • First negative number: -15 (because index 4 is still the first in the deque).
   • Output so far: -1 -1 -7 -15
5. Window 5: Indices 4 to 6 ([-15, 30, 16])
   • Remove indices that are out of the window:
     • Index 4 is still in the window.
   • The deque now contains [4] (pointing to -15).
   • Add the new element arr[6] = 16, which is not negative.
   • The deque still contains [4].
   • First negative number: -15 (because index 4 is still the first in the deque).
   • Output so far: -1 -1 -7 -15 -15
6. Window 6: Indices 5 to 7 ([30, 16, 28])
   • Remove indices that are out of the window:
     • Index 4 is out of the window, so we remove it.
   • The deque is now empty.
   • Add the new element arr[7] = 28, which is not negative.
   • The deque is empty, so no negative number is found.
   • First negative number: 0 (since the deque is empty).
   • Output so far: -1 -1 -7 -15 -15 0

Final Output:

-1 -1 -7 -15 -15 0

Time Complexity:

• O(n), where n is the length of the array.

Conclusion:

• Brute Force Approach: O(n * k) — Simply iterate over each window and find the first negative number.
• Better Approach: O(n) — Use a deque to keep track of negative numbers in the window, leading to a much faster solution.